INRAE
Python v3.2
Un modèle biophysique et biogéochimique de fonctionnement des forêts de production.
Le modèle GO+ est un modèle de croissance, de production et de gestion forestière représentant les principaux processus biophysiques et biogéochimiques d'une forêt gérée. Son approche de modélisation est de type mécaniste : elle représente les processus impliqués dans le fonctionnement de l’écosystème et les opérations de sylviculture. Le modèle GO+ version 3.0 est publié et décrit dans Moreaux et al. (2020) et le code (python 3.0) est déposé sur github et l'entrepot de données data-Inrae. La version 3.1 du modèle développée avec le projet BIO-SYLVE (Ademe) sera publiée prochainement.
Le modèle considère une unité spatiale correspondant à une zone homogène de végétation forestière, typiquement un hectare, et décrit son fonctionnement et la dynamique de croissance du peuplement (régénération, croissance et mortalité des arbres individuels) pour l’ensemble du cycle de vie de l’écosystème forestier (50-300 ans). Le modèle décrit les échanges de masse (carbone, eau) et d'énergie (rayonnement, chaleur, vent) dans le système sol-végétation-atmosphère. Ces échanges déterminent le bilan d’énergie, les cycles du carbone et de l'eau. Il prend en compte les processus de transfert turbulent, transfert radiatif, l'évapo-transpiration, la photosynthèse, la respiration, la répartition du carbone dans les plantes, la croissance, la phénologie, la mortalité et les transformations et minéralisation du carbone dans le sol.
La végétation est décrite en deux couches ou strates, les arbres et la végétation accompagnatrice. Les deux couches de végétations sont dynamiques : les parties aériennes et souterraines des plantes suivent un cycle phénologique incluant les phases de dormance, débourrement, croissance et mortalité. Ce développement est rythmé par l’évolution de la température et du rayonnement solaire. La mortalité est déclenchée par les stress hydriques ou thermiques, les opérations sylvicoles et les récoltes.
Les effets sur l’écosystème des principales opérations incluses dans un itinéraire technique sylvicole donné sont pris en compte : préparation du sol, gestion du sous-étage, éclaircies, recépage, coupes à blanc.
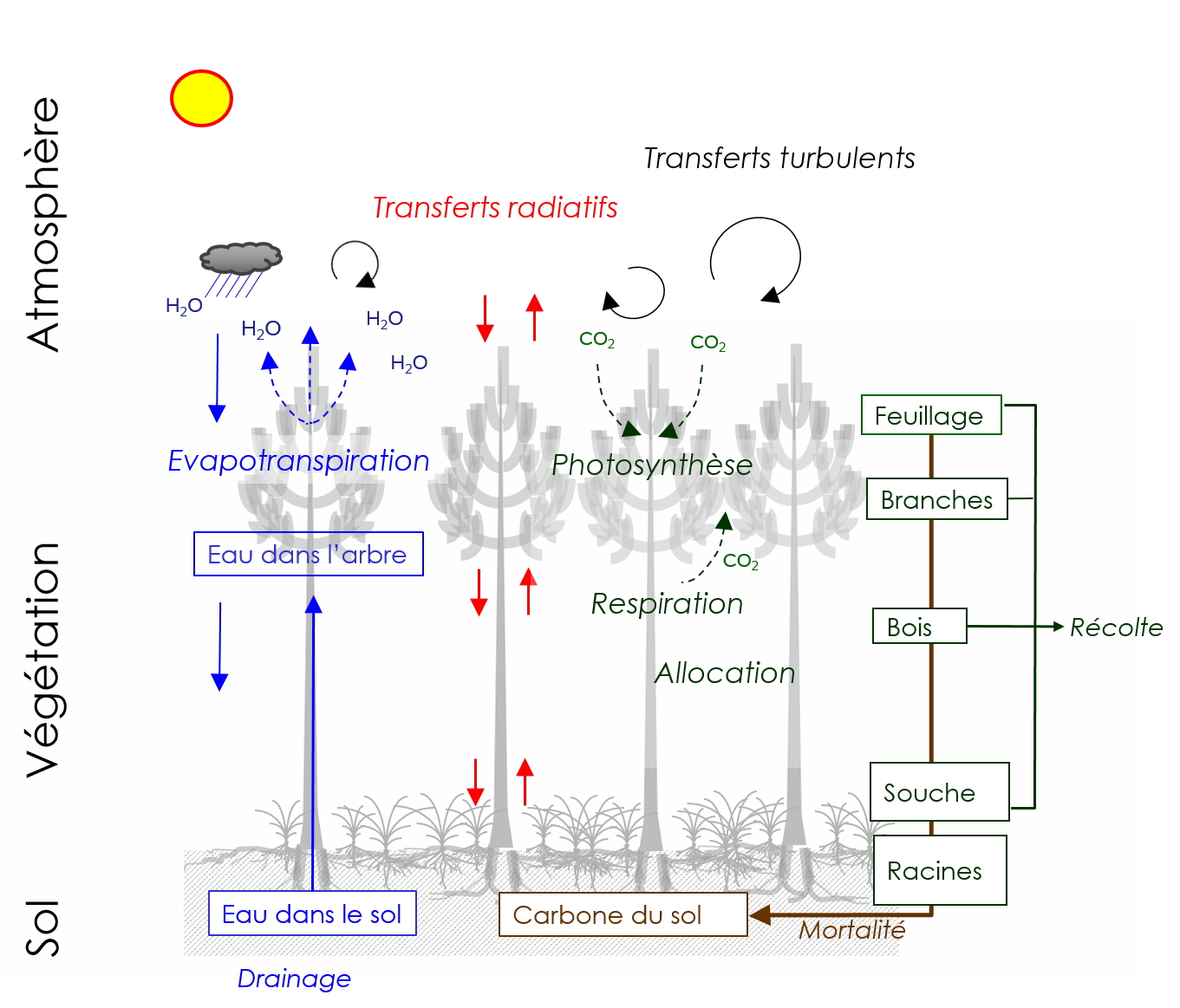
PROCESSUS
Cliquez sur un processus pour en savoir plus.
Transferts radiatifs et bilan d’énergie.
Le microclimat et les flux radiatifs de grandes et courtes longueurs d'onde sont évalués en fonction d'un schéma simple basé sur la loi de Beer-Lambert et séparant les fractions ombrée et ensoleillée du feuillage pour chacune des couches (dePury et Farquhar, 1997). Ce schéma tient compte des fractions directes et diffuses du rayonnement solaire incident (Spitters et al. 1986) et de la rediffusion du rayonnement au premier ordre. Le bilan d’énergie et le calcul de la température du feuillage sont résolus au pas de temps horaire et pour chaque compartiment. A partir du bilan d’énergie, la température moyenne de chaque couche est calculée au pas horaire.Évapotranspiration.
L’évapotranspiration est le flux de vapeur d’eau transféré depuis l’écosystème vers l’atmosphère. Ce flux représente plusieurs dizaines de mètres cubes d’eau par hectare de forêt annuellement. Il est exprimé en kg d’eau évaporé par unité de surface (m²) et de temps (heure). Un kilogramme d’eau recouvrant une épaisseur de 1 mm sur une surface de 1 m, il est couramment aussi exprimé en mm par heure (évapotranspiration). Il inclut deux composantes :- L’évaporation depuis les surfaces mouillées et le sol. Durant un épisode de précipitations, une fraction des précipitations est retenue par le feuillage, les branches et le tronc des arbres (interception). Une partie de l’eau ainsi interceptée est ré-évaporée. Dans GO+, la quantité d’eau liquide retenue sur le feuillage et à la surface du sol durant les épisodes pluvieux est calculée au pas horaire à partir du bilan hydrique de la surface de feuillage et des éléments ligneux (troncs, branches) (Gash et al. 1979). L’autre source d’évaporation directe est le sol.
- La transpiration, depuis le couvert sec, correspond à un transport de vapeur depuis l’intérieur des feuilles vers l’atmosphère et s’opère à travers les pores stomatiques pour l’essentiel. La transpiration végétale est régulée par l’indice foliaire et le fonctionnement des stomates qui régulent la diffusion de la vapeur d’eau et au CO2. Celle-ci est modélisée en tenant compte des différents facteurs contrôlant l’indice foliaire et l’ouverture des stomates :
- Rayonnement solaire incident, température et humidité de l’air.
- Concentration en CO2 de l’air.
- État hydrique des feuilles (potentiel hydrique foliaire), qui dépend de la hauteur des arbres et de la disponibilité de l’eau dans le sol.
Eau dans l’arbre.
L'état hydrique du feuillage est calculé en utilisant un schéma de transfert hydraulique simple reliant l’eau du sol aux feuilles par un circuit hydraulique comprenant deux résistances en série, sol–racine et racine–feuille, et une capacitance. Le potentiel hydrique moyen du feuillage est ainsi calculé au pas horaire. Il définit l’état énergétique de l’eau dans la plante et exprime l’état de stress hydrique de la plante. Le potentiel hydrique exerce un contrôle étroit sur l’ouverture des stomates des feuilles, et, par suite, la transpiration des arbres, la température du feuillage, la photosynthèse et la respiration du feuillage.Eau dans le sol.
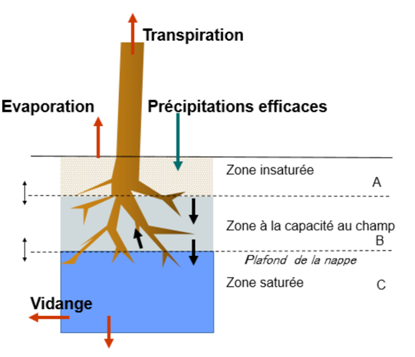 Le sol est décrit comme une cascade de trois réservoirs correspondant respectivement à :
Le sol est décrit comme une cascade de trois réservoirs correspondant respectivement à :
- A, une zone superficielle sous la capacité au champ (beige)
- B, une zone à la capacité au champ (bleu pâle).
- C, une zone saturée (nappe phréatique) (bleu soutenu).
Photosynthèse et respiration des plantes.
Le calcul de la photosynthèse, ou production primaire brute, des deux couches de végétation est basé sur le modèle biochimique de Farquhar et al. (1980) le plus couramment utilisé. Partant de la cinétique enzymatique des réactions du cycle de Calvin et du transfert d’énergie réductrice créée par transformation de l’énergie lumineuse, il décrit la vitesse de fixation du carbone par le feuillage. La photosynthèse est donc exprimée en grammes de carbone-CO2 absorbé par unité de surface de sol et par unité de temps, gC m-2 jour-1. Ce formalisme prend en compte de façon réaliste les effets de la température du feuillage, de la concentration en CO2 et du contrôle stomatique ainsi que du rayonnement incident.
La respiration de la plante est estimée pour chaque partie de la plante comme la somme de deux termes.
- La respiration de maintenance, dépendante de la température, et proportionnelle à la concentration en azote de la biomasse vivante (Ryan, 1992, Dufrêne et al. 2005). La respiration foliaire est partiellement inhibée par le rayonnement solaire.
- La respiration de croissance calculée comme le coût de construction des constituants biochimiques de la plante. Ici, ce coût est fixé à 28% du carbone utilisé pour la croissance.
Elle est exprimée comme la photosynthèse en grammes de carbone-CO2 émis par unité de surface de sol et par unité de temps.
Allocation du carbone et croissance.
L'attribution de la production primaire en carbone à chaque arbre se fait au pro rata de sa contribution à l’indice foliaire. Le carbone disponible pour la croissance est réparti entre biomasses aérienne et souterraine de l’arbre selon un indice de stress (Landsberg et Waring, 1997) calculé comme le rapport entre la transpiration annuelle effective et la transpiration annuelle potentielle : plus le stress est fort, plus l’allocation aux racines est élevée.
La biomasse aérienne est distribuée entre tronc, feuillage et branches selon les relations allométriques connues pour chaque espèce (Gholz, 1979, Shaiek et al. 2011, Wutzleret & al. 2007, Le Moguedec et Dhôte 2012, Achat et al. 2018). La biomasse souterraine est de même distribuée entre les différents compartiments racinaires (racines fines, souche et pivot, …) (Achat et al. 2018).
Une mortalité naturelle stochastique fixe ou variable (insectes, pathogènes) peut être prescrite.GO+ simule par ailleurs une mortalité "climatique" qui affecte les individus dont le bilan annuel en carbone est négatif. Il s'agit ici des indivdus dont le besoin en glucides pour la respiration de maintenance excède la production photosynthétique annuelle. Cette mortalité climatique intervient durant les années à fort déficit hydrique.
Carbone du sol.
La dynamique du carbone du sol dérive du modèle Roth-C v6.3 (Coleman et Jenkinson, 1996) qui est appliqué ici en traitant l’ensemble du carbone du sol comme un ensemble de cinq pools et en conservant les valeurs des paramètres proposées par ses auteurs. La minéralisation du carbone du sol dépend ainsi de facteurs externes (température et humidité du sol), de la décomposabilité des apports en matière organique et de la teneur en argile du sol. L’effet des opération de travail du sol est simulé en accélérant la vitesse de minéralisation du carbone dans la fraction du sol affectée pour une durée de 12 semaines.
.
Eau dans l'arbre.
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. Neque viverra justo nec ultrices dui. Id volutpat lacus laoreet non curabitur gravida arcu ac tortor. Amet risus nullam eget felis eget nunc lobortis mattis. Lorem dolor sed viverra ipsum nunc aliquet. Quis enim lobortis scelerisque fermentum dui faucibus.Phénologie.
Pour les arbres, seul le feuillage présente un cycle annuel phénologique incluant débourrement, croissance et mortalité. La croissance des autres parties de la plante n’est résolue qu’au pas de temps annuel. Selon l’essence considérée, plusieurs modèles de phénologie foliaire sont actionnables : une somme de degrés-jour (Desprez-Loustau et Dupuis, 1994), le modèle séquentiel de Kramer (1994), ou le modèle alterné de Harrington (2010) qui sont bien adaptés au Pins, Hêtre et Douglas respectivement. La calibration des paramètres pour les essences métropolitaines s’est appuyée sur la littérature disponible et d’observations provenant du réseau Renecofor et de réseaux phénologiques aux Pays-Bas et en Allemagne.
Pour la végétation accompagnatrice, la croissance de chacune des parties de la plante, feuille, organes pérennes ou racines, est résolue au pas journalier. La phénologie répond à un modèle simple d’accumulation de degrés jours pour le démarrage de la croissance. La croissance potentielle est modélisée selon une courbe sigmoïde. La croissance réalisée est modulée par le carbone disponible: elle est ralentie par les stress hydrique et thermique. La mortalité des parties caduques en fin de saison est déclenchée soit par une accumulation de stress hydrique ou thermique soit par une durée limite de végétation.
Production et récolte
Le volume et la biomasse récoltables sur pied (découpe 7cm) sont calculés annuellement. Les fractions récoltées et exportées hors parcelle (tronc, souche, branche, feuillage) sont simulées conformément à l’ITK choisi. Les résidus de récolte retournent au sol. Le sous-étage n’est pas récolté mais peut être contrôlé par débroussaillage.Gestion sylvicole.
Les itinéraires techniques (ITK) sont une série d’opérations qui affectent le peuplement principal, le sous-étage et le sol. Ces opérations sont prescrites selon les combinaisons voulues de techniques de régénération, dégagement, éclaircies et récoltes. Elles peuvent être déclenchées par différents critères :- Âge des arbres.
- Valeurs seuil de variables dendrométriques comme le diamètre ou la hauteur moyenne des troncs.
- Indice de compétition (RDI, Le Moguedec et Dhôte, 2012)
Peuplement principal
Les valeurs initiales de densité et la circonférence individuelle de chaque arbre sont prescrites. Deux régimes de conduite sont décrits dans la version 27.0 de GO+, la futaie régulière et le taillis.- La conduite en futaie régulière est définie par :
- Les critères de déclenchement de chaque éclaircie et de la coupe finale. Ces critères sont définis par les experts en sylviculture de chacune des essences. Ils peuvent être l’âge, un indice de compétition (RDI), la circonférence moyenne ou dominante, ou la hauteur moyenne ou dominante, la surface terrière...ou encore toute combinaisonde ces critères.
- Le critère de sélection des arbres récoltés: les éclaircies peuvent être effectuées par le haut (les plus gros arbres), par le bas (les plus petits arbres) ou de façon aléatoire.
- Les fractions récoltées qui peuvent être le tronc sur écorce, la souche, les branches, le feuillage ou les grosses racines.
- Le régime de taillis est caractérisé par le critère de déclenchement de la coupe, la densité des souches, le nombre de brins sélectionnés par souche et le nombre de recépées successives.
Sous–étage.
La biomasse du sous-étage est détruite partiellement ou totalement à chaque éclaircie et coupe. Elle est aussi détruite partiellement ou totalement par les opérations de dégagement qui peuvent être prescrites avant ou après régénération. La fraction de biomasse détruite par ces opérations peut prendre des valeurs différentes pour les parties aériennes et racinaires. Sol. Les opérations forestières affectent le sol par les retours au sol de matière organique morte provenant de la destruction du sous étage ou les résidus de récolte et des parties non récoltées du peuplement principal. Les opérations de travail et préparation du sol affectent aussi les processus de transformation et minéralisation de la matière organique du sol.Sol
Le modèle calcule la fraction de carbone du sol affectée par les opérations forestières (labour, disquage, rouleau lourd…). Pour cette fraction, la constante de décomposition et le facteur de minéralisation du carbone en CO2 sont modifiés comme suit:- la vitesse de décomposition de la matière organique est multipliée par 3.
- La minéralisation du carbone en CO2 est portée à 100%, contre 80% sans travail du sol.
Références.
Achat, D. L., Martel, S., Picart, D., Moisy, C., Augusto, L., Bakker, M. R., and Loustau, D. (2018) Modelling the nutrient cost of biomass harvesting under different silvicultural and climate scenarios in production forests, For EcolManag, 429, 642-653.
Arrouays, D. and Pelissier, P. (1994) Changes in Carbon Storage in Temperate Humic Loamy Soils after Forest Clearing and Continuous Corn Cropping in France, Plant and Soil, 160, 215-223.
Bellassen, V., le Maire, G., Guin, O., Dhote, J. F., Ciais, P., and Viovy, N. (2011) Modelling forest management within a global vegetation model-Part 2: Model validation from a tree to a continental scale, Ecol Model, 222, 57-75.
Ciais, P., Loustau, D., Bosc, A., Ogée, J., Dufrêne, E., François, C., Viovy, N., and Delage, F. (2010)How will the production of French forests respond to climate change? An integrated analysis from site to country scale. In: Forests, carbon cycle and climate change, Loustau, D. (Ed.), Quae, Paris.
Coleman K., and Jenkinson:, D.D.: RothC - 26.3 –(1996) A model for the turnover of carbon in soil. , in: Evaluation of soil organic matter models using existing, long-term datasets., edited by: Powlson D.S., Smith P., and J.U., S., NATO ASI Series I, Springer Verlag, Heidelberg, Germany, 237-246.
Davi, H., Dufrêne, E., Granier, A., Le Dantec, V., Barbaroux, C., François, C., and Bréda, N. (2005) Modelling carbon and water cycles in a beech forest, Ecol Model, 185, 387-405.
DePury, D. G. G. and Farquhar, G. D. (1997)Simple scaling of photosynthesis from leaves to canopies without the errors of big-leaf models, Plant Cell Environ, 20, 537-557.
Desprez-Loustau, M. L. and Dupuis, F. (1994) Variation in the phenology of shoot elongation between geographic provenances of maritime pine (Pinus pinaster) - implications for the synchrony with the phenology of the twisting rust fungus, Melampsora pinitorqua, Ann Sci Forest, 51, 553-568.
Dufrêne, E., Davi, H., François, C., Le Maire, G., Le Dantec, V., and Granier, A. (2005) Modelling carbon and water cycles in a beech forest. Part I: Model description and uncertainty analysis on modelled NEE, Ecol Model, 185, 407-436. https://doi.org/10.1016/j.ecolmodel.2005.01.004
Farquhar, G. D., von Caemmerer, S., and Berry, J. (1980) A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species, Planta, 149, 78-90.
Gash, J. H. C. (1979) Analytical model of rainfall interception by forests, Q J Roy Meteor Soc, 105, 43-55, 10.1002/qj.49710544304.
Harrington, C. A., Gould, P. J., and St Clair, J. B. (2010)Modeling the effects of winter environment on dormancy release of Douglas-fir, Forest EcolManag, 259, 798-808, 10.1016/j.foreco.2009.06.018, 2010
Jolivet, C. (2000)Le carbone organique des sols des Landes de Gascogne variabilité spatiale et effets des pratiques sylvicoles et agricoles, Thèse de doctorat en Sciences biologiques fondamentales et appliquées, Université de Bourgogne, Dijon, 306p.
Jones, H.G. (1992) Plants and microclimate. A quantitative approach to environmental plant physiology, Cambridge University Press, Cambridge.
Le Moguedec, G. and Dhote, J. F. (2012) Fagacees: a tree-centered growth and yield model for sessile oak (Quercus petraea L.) and common beech (Fagus sylvatica L.). Ann For Sci, 69, 257-269.
Kramer, K. (1994) Selecting a Model to Predict the Onset of Growth of Fagus-Sylvatica, Journal of Applied Ecology, 31, 172-181.
Landsberg, J. J. and Waring, R. H. (1997)A generalised model of forest productivity using simplified concepts of radiation-use efficiency, carbon balance and partitioning, For EcolManag, 95, 209-228.
Loustau, D., Bosc, A., Colin, A., Ogee, J., Davi, H., Francois, C., Dufrene, E., Deque, M., Cloppet, E., Arrouays, D., Le Bas, C., Saby, N., Pignard, G., Hamza, N., Granier, A., Breda, N., Ciais, P., Viovy, N., and Delage, F. (2005) Modeling climate change effects on the potential production of French plains forests at the sub-regional level, Tree Physiol, 25, 813-823. https://doi.org/10.1093/treephys/25.7.813
Mohren, G. M. J., and Bartelink, H. H. (1990)Modeling the effects of needle mortality-rate and needle area distribution on dry-matter production of Douglas-fir,Neth J AgrSci, 38, 53-66.
Moreaux, V., Martel, S., Bosc, A., Picart, D., Achat, D., Moisy, C., Aussenac, R., Chipeaux, C., Bonnefond, J.-M., Trichet, P., Vezy, R., Badeau, V., Longdoz, B., Granier, A., Roupsard, O., Nicolas, M., Pilegaard, K., Matteucci, G., Jolivet, C., Black, A. T., Picard, O., and Loustau, D.: Energy, water and carbon exchanges in managed forest ecosystems: description, sensitivity analysis and evaluation of the INRAE GO+ model, version 3.0, Geosci. Model Dev. Discuss., https://doi.org/10.5194/gmd-2020-66, in review, 2020.
Moreaux, V. (2012) Observation et modélisation des échanges d'énergie et de masse de jeunes peuplements forestiers du Sud-Ouest de la France., Ph. D.Thesis., Ecole Doctorale 304 "Sciences et Environnements", Thématique "Physique de l'Environnement", Université de Bordeaux-1, Bordeaux, 262 pages pp., 2012. https://www.theses.fr/2012BOR14506
Nakai, T., Sumida, A., Daikoku, K. i., Matsumoto, K., van der Molen, M. K., Kodama, Y., Kononov, A. V., Maximov, T. C., Dolman, A. J., Yabuki, H., Hara, T., and Ohta, T. (2008) Parameterisation of aerodynamic roughness over boreal, cool- and warm-temperate forests, Agr Forest Meteorol, 148, 1916-1925, https://doi.org/10.1016/j.agrformet.2008.03.009, 2008.
Ryan, M. G. (1991) Effects of climate change on plant respiration, Ecol Appl, 1, 157-167, 1991.
Shaiek, O., Loustau, D., Trichet, P., Meredieu, C., Bachtobji, B., Garchi, S., and El Aouni, M. H. (2011) Generalized biomass equations for the main above-ground biomass components of maritime pine across contrasting environments, Ann Forest Sci, 68, 443-452.
Spitters, C. J. T., Toussaint, H. A. J. M., and Goudriaan, J. (1986) Separating the diffuse and direct component of global radiation and its implications for modeling canopy photosynthesis Part I. components of incoming radiation, Agric For Meteorol, 38, 217-229.
Wutzler, T., Wirth, C., and Schumacher, J. (2008) Generic biomass functions for Common beech (Fagus sylvatica) in Central Europe: predictions and components of uncertainty, Can J Forest Res, 38, 1661-1675, 10.1139/x07-194. https://www.nrcresearchpress.com/doi/full/10.1139/X07-194